Analiza statystyczna zmienności na rynku Forex

Analiza statystyczna zmienności na rynku Forex pozostaje wciąż szeroko nieporuszanym tematem zarówno przez traderów jak i analityków. Każdy trader na rynku mierzy się z szeregiem czynników, które determinują jego skuteczność. Jednym z najważniejszych aspektów jest właśnie zmienność, która charakteryzuje zakres wahań notowań danego instrumentu w określonym okresie czasu. Inwestorzy będący uczestnikami rynku od wielu lat z pewnością pamiętają okresy, gdy zmienność była niezwykle wysoka oraz takie, gdy notowania poruszały się w bardzo wąskim paśmie przez wiele dni.

Czym jest zmienność? Czy jest ona zagrożeniem, czy też szansą? Czy zmienność da się ubrać w konkretne schematy? Czy po silnych wzrostach następują spadki? Czy po silny spadkach występują wzrosty? Na te pytania wspólnie z Szymonem Nowakiem postaraliśmy się odpowiedzieć, analizując historyczne notowania najpopularniejszych par walutowych. W pierwszej części Szymon zajął się zmianami dziennymi, jakim podlegały EUR/USD, GBP/USD, USD/JPY oraz AUD/USD, z kolei w drugiej części ja zrobiłem to samo dla interwałów tygodniowych. Na zakończenie porównałem zmienność tygodniową między wszystkimi walutami, by określić na których możemy liczyć na największe zmiany, a na których wielkość zmiany jest najbardziej przewidywalna.

Pod nieco innym kątem na zmienność spojrzał już Damian Nowiszewski, który w swoim tekście zwracał uwagę na różne zachowanie par walutowych w czasie poszczególnych sesji inwestycyjnych.

Analiza statystyczna zmienności na rynku Forex

Aby w jak najbardziej naukowy sposób przeanalizować zmienność występującą na rynku Forex, należy wykorzystać odpowiednie miary statystyczne. Oferuje je dział zwany statystyką opisową, na którą składają się miary opisujące wybrane zbiory wyników. Należy do nich przede wszystkim jeden z najpopularniejszych parametrów – iloraz sumy wyników i ich liczby – a więc średnia arytmetyczna.

Mimo, że jest ona szeroko wykorzystywana, a jej obliczenie nie nastręcza problemów, nierzadko zdarza się, że wyniki nietypowe (wyjątkowe zdarzenia, które akurat znalazły się w naszej próbie) znacząco zniekształcają obraz, jaki wskazuje średnia arytmetyczna. Na przykład, w firmie, w której pracuje pięciu robotników zarabiających 2 000 PLN i jeden prezes, którego pensja wynosi 100 000 PLN, średnie zarobki wynoszą prawie 20 000 PLN, jednak intuicyjnie wiemy, że taka średnia nie oddaje rzeczywistości we właściwy sposób.

Ze znacznymi odchyleniami (na FX przykładem niech będzie styczniowa decyzja SNB) do czynienia mamy praktycznie w każdym zbiorze i z tego też powodu warto je wyłączyć z próby, by nie zniekształcały typowych wyników. Można to zrobić albo w sposób subiektywny (można przyjąć, że to co zrobił SNB nie powtórzy się w przyszłości, a było to sytuacją całkowicie wyjątkową), albo wyłączyć z próby określony procent skrajnych przypadków.

W tym momencie może powstać pytanie – dlaczego wyłączać z badań tego typu wyniki, w końcu chcemy poznać pełną charakterystykę notowań wybranej waluty. Naturalnie, jednak musimy pamiętać o dwóch rzeczach. Po pierwsze, analiza statystyczna ma nam dać informacje o typowych ruchach kursów, więc nie możemy wyciągać wniosków na podstawie nietypowych przypadków. Po drugie, na rynku finansowym po prostu raz na bardzo rzadki okres zdarzają się tego typu wydarzenia i analiza statystyczna nas przed nimi nie ochroni, więc z tym faktem należy się po prostu pogodzić.

Innym sposobem na zmierzenie tendencji centralnej pewnego zbioru, jest uszeregowanie wyników w kolejności rosnącej i znalezienie wartości znajdującej się dokładnie w środku. Nazywa się ona medianą a jej interpretacja jest bardzo prosta – mediana informuje, że nie więcej niż 50% wyników jest niższych i nie więcej niż 50% wyników jest wyższych niż jej wartość. Czym różni się ona od średniej? We wskazanym wcześniej przykładzie mediana wskazałaby wartość dokładnie 2000 PLN, a więc znacznie lepiej odwzorowałaby rzeczywistość. Jeżeli mediana jest niższa od średniej, to oznacza, że w zbiorze występuje znaczna ilość wyników niższych od średniej, jednak zdarzają się też znacznie zawyżone przypadki.

Statystycy stosują również miarę zwaną dominantą (czyli wartość najczęstszą), jednak w przypadku zmian dziennych czy tygodniowych na Forexie, gdzie praktycznie nie zdarzają się takie same ruchy, byłaby trudna do zastosowania. Można naturalnie podzielić wszystkie wyniki na odpowiednie przedziały i wybrać ten, który zawierają najwyższą liczbę przypadków.

Jeżeli już znamy generalną tendencję wyników, można sprawdzić w jakim stopniu poszczególne wartości odchylają się od swojej średniej. W tym celu stosuje się odchylenie standardowe, które, w ogromnym uproszczeniu, wskazuje średnią różnicę wszystkich wyników i ich średniej. Odchylenie powie nam więc, o ile średnio rzecz biorąc pipsów, każdy wynik różnił się od średniej.

Miara ta dobrze odwzorowuje zmienność, jednak nie sprawdza się w przypadku porównywania wyników na różnych parach walutowych. Odchylenie standardowe jest bowiem wartością bezwzględną – odchylenie 50 pipsów na parze, której średnie ruchy wynoszą 80 pipsów wskazuje na ogromną zmienność, podczas gdy odchylenie na poziomie 100 pipsów w przypadku pary, która średnio zmienia swój kurs o 300 pipsów, wskaże znacznie niższą zmienność.

Z tego też powodu, wykorzystuje się współczynnik zmienności, będący iloczynem odchylenia standardowego i średniej, a wskazujący jaką częścią średniej jest odchylenie wyników. Współczynnik zmienności na poziomie 0,4, przy średniej 100 pipsów powie nam, że kurs danej pary walutowej zmienia się średnio o 100 pipsów i możemy oczekiwać około 40-procentowego odchylenia.

Co ważne jednak, współczynnik zmienności pozwoli nam stwierdzić, że jedne pary są bardziej zmienne od innych, niezależnie od tego, o ile średnio zmieniają się ich kursy.

Niezależnie od tego jakie zastosujemy miary, i z jak wyrafinowanych metod statystycznych skorzystamy, należy zawsze pamiętać do czego służy nam statystyka opisowa. Charakteryzuje ona dotychczasowe wyniki i, choć bardzo byśmy tego chcieli, niekoniecznie przekłada się na to, co będzie się działo w przyszłości. Możemy oczywiście liczyć na to, że wybrana para nie zmieni swoich własności tradingowych z dnia na dzień, nie zaszkodzi jednak zaktualizować swoich wyników, gdy minie pewien czas.

Zmienność dzienna

Na podstawie danych dziennych (od początku 2014 roku) oczyszczonych z notowań niedzielnych sprawdziłem, w jakich zakresach poruszają się cztery pary walutowe – EURUSD, GBPUSD, USDJPY oraz AUDUSD oraz odpowiedziałem na postawione sobie pytanie – czy po nadzwyczajnie dużych wzrostach/spadkach notowania w następnym dniu spadają/rosną. Bardzo często popularne przekonania obecne wśród inwestorów niekoniecznie mają przełożenie na rzeczywistość. Czy tak też jest i tym razem?

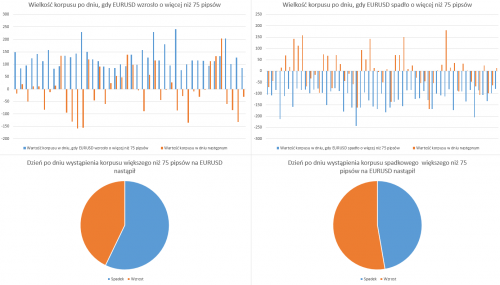
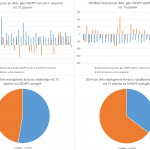
Zaczynając od EURUSD można zauważyć, że najczęściej zakres dziennej świecy liczonej od minimum do maksimum wynosi między 50 a 100 pipsów. Rozpatrując już jednak sam korpus, czyli zakres pomiędzy otwarciem a zamknięciem świecy, widać iż ma on najczęściej wartość do 25 pipsów. Co ciekawe, korpusy świec spadkowych mają zdecydowanie bardziej widoczny ogon w przedziale od 150 do 200 pipsów. Współgra to z praktyką, gdyż często obserwuje się na rynku, iż spadki są bardziej dynamicznie niż wzrosty i to potwierdza powyższy wykres.

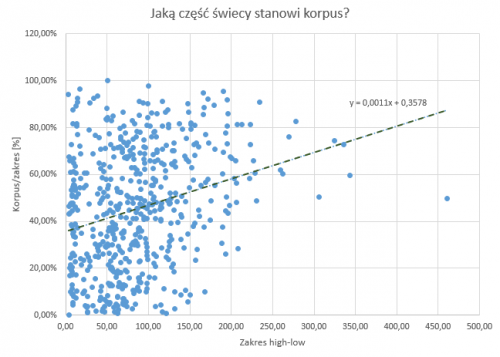
Nie można się jednak doszukać jasnej zależności pomiędzy zakresem cenowym świecy a wielkością korpusu. Widocznie jednak w wypadku ekstremalnie dużych zakresów korpus tylko w nielicznych wypadkach stanowi więcej niż 80% zakresu.

Biorąc pod uwagę, że korpus w wysokości większej niż 75 pipsów występuje stosunkowo rzadko, czyli można go uznać za wyjątkowo duży, sprawdziłem ponadto czy po wystąpieniu takiego korpusu następnego dnia dzienna świeca jest spadkowa, czy też wzrostowa. Okazuje się, że statystyka potwierdza w tym wypadku intuicję. Po wystąpieniu znaczących wzrostów, następnego dnia na EURUSD najczęściej świeca jest spadkowa. Po wystąpieniu znaczących spadków, kolejna świeca jest natomiast wzrostowa. Jak widać na powyższym wykresie, przewaga takiej zależności nie jest znacząca, lecz jednak zauważalnie występuje.

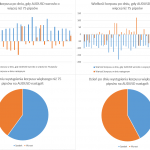
Wykresy powstałe w wyniku przeprowadzonego badania dla par GBPUSD, USDJPY oraz AUDUSD możesz zobaczyć poniżej i wyciągnąć samodzielnie analogiczne wnioski.

 

Zmienność tygodniowa

W przypadku zmienności tygodniowej interesują nas nieco inne informacje niż te, których szukaliśmy w notowaniach dziennych. Z tego też powodu przeanalizowane one muszą zostać w nieco inny sposób.

Dane o zmianach tygodniowych dotyczą okresu od połowy 2013 roku do początku października 2015 roku.

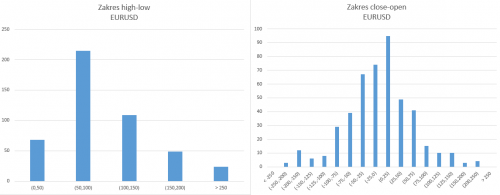
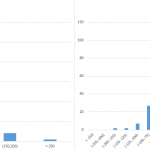
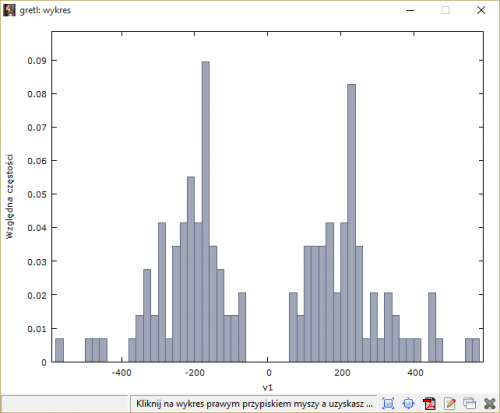
Po pierwsze warto wiedzieć jak kształtuje się rozkład częstości poszczególnych wyników. W tym celu każda próba (składająca się z różnic między High i Low, uwzględniających czy tydzień był wzrostowy czy spadkowy) podzielona została na odpowiednie przedziały o szerokości 20 pipsów. Następnie na tej podstawie sporządzony został poniższy wykres.

Pokazuje on jak rozkłada się zmiana w pipsach w poszczególnych tygodniach. Na skali poziomej rozłożone zostały przedziały, na skali pionowej z kolei wskazana została częstość (udział) wyników z danego przedziału w całej próbie. Z wykresu dowiadujemy się na przykład, że w przypadku spadków ruchy wynoszą najczęściej między 160 a 180 pipsów i jest to aż prawie 9% całości wyników. W przypadku wzrostów najliczniejszym przedziałem jest z kolei 220 – 240 i stanowi on prawie 8,5% puli.

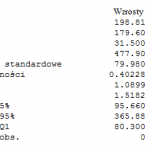
Oprócz tego, warto przeanalizować statystyki opisowe dla obydwu grup – wzrostów oraz spadków – by sprawdzić, czy zbiory te w jakiś sposób się między sobą różnią. Informacje te znajdziemy poniżej.

W przypadku Eurodolara widać, że charakterystyka zarówno wzrostów jak i spadków pozostaje podobna, a delikatne różnice między nimi niemal nie mają dla nas znaczenia. Po pierwsze, zarówno średnia jak i mediana są nieznacznie wyższe w przypadku wzrostów, co oznacza, że świece wzrostowe są zwykle nieco większe, niż świece spadkowe. Są przy tym nieco bardziej zmienne, na co wskazuje wyższy współczynnik zmienności [%]. Skośność informuje nas z kolei o asymetrii rozkładu, a im jej dodatnia wartość jest wyższa, tym więcej wyników jest niższych od średniej. W powyższym przypadku wyższa skośność dla spadków informuje nas o tym, że to dla spadków więcej wyników znalazło się poniżej średniej (która w dodatku jest niższa), a więc to wzrosty okazują się przeważnie bardziej zdecydowane i mocniejsze.

Kurtoza informuje nas z kolei o zagęszczeniu wyników wokół średniej (im wyższa, tym więcej wyników znajduje się blisko średniej). Tutaj również widzimy (i potwierdza to analiza wizualna wykresu), że to wzrosty są bardziej “rozrzucone” po skali, z kolei wartości spadków rozkładają się nieco bliżej swojej średniej, są więc nieco lepiej przewidywalne.

Nieco odmienne wnioski, w dokładnie ten sam sposób, wyciągnąć można na podstawie tych samych danych dla pozostałych głównych par walutowych.

Statystyka zmian tygodniowych najpopularniejszych walut

Na koniec postanowiłem zmierzyć zmienność na poszczególnych walutach (w parze z dolarem – z tego powodu jego w tym zestawieniu zabrakło) i porównać je między sobą. Dzięki temu będziemy wiedzieć, na której z walut możemy liczyć na największe ruchy i która jest najbardziej zmienna. Analiza dotyczyć będzie oczywiście jedynie par z dolarem, jednak można przyjąć, że podobną specyfikę waluty te przyjmują na innych parach. Co ważne, w poniższych porównaniach zestawione zostały bezwzględne ruchy, nieuwzględniające czy danego dnia nastąpił spadek czy wzrost.

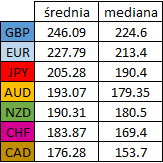Jeżeli chodzi o generalną tendencję, największe ruchy zauważyć możemy na funcie oraz euro, gdzie zarówno średnie ruchy jak i ich mediana wskazują wartości powyżej 200 pipsów. Co ważne, na kształt tabeli nie wpłynęła wysokość kursów (teoretycznie, im wyższy kurs, tym większe nominalne zmiany powinniśmy obserwować). Walutami których tygodniowe zmiany są najniższe okazały się frank szwajcarski oraz dolar kanadyjski, jednak w żadnym przypadku nie trudno się temu dziwić.

Przez większość czasu frank ulegał takim samym zmianom jak euro (obydwa kursy były powiązane), przy czym kurs franka w dolarach był znacznie niższy, więc, o ile procentowe zmiany mogły być podobne, w pipsach widać znaczną różnicę. Dolar kanadyjski to z kolei waluta silnie uzależniona nie tylko od kondycji swojego kraju, ale i Stanów Zjednoczonych, czyli największego partnera handlowego Kanady. Stąd też, obydwie waluty reagowały podobnie na ten sam zestaw danych.

We wszystkich przypadkach naturalnie powtarza się relacja średnia > mediana, co jasno wskazuje na fakt, że rozkłady te cechują się prawą asymetrią (większość wyników jest niższa od średniej, jednak występują nieliczne przypadki znacznie odbiegające od typowego zachowania).

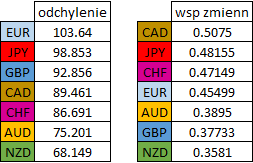W przypadku odchyleń poszczególnych wyników od średniej, największego rozstrzału możemy się spodziewać w przypadku euro, którego tygodniowe zmiany odchylały się średnio rzecz biorąc o ponad 100 pipsów od swojej średniej. Oznacza to, że jeżeli w przypadku tej waluty oczekujemy ruchu zawsze na poziomie około 230 pipsów (zaokrąglona średnia) to średnio pomylimy się o około 100 pipsów. Co jednak ważne, tak jak wspomniałem wcześniej, wysokie odchylenie nie oznacza, że dana waluta rzeczywiście jest bardziej zmienna od innej, gdyż, jeżeli w przypadku wybranej waluty (czy jakiejkolwiek innej zmiennej) obserwujemy wyższą średnią, możemy oczekiwać, że również odchylenie standardowe będzie wyższe. Stąd też, do takiego porównania stosuje się współczynnik zmienności, który niejako standaryzuje uzyskane dane.

W takim zestawieniu widzimy z kolei, że to dolar kanadyjski jest najbardziej zmienną walutą, mimo że to w jego przypadku zaobserwowaliśmy wcześniej najniższą średnią. Oznacza to, że nasze oczekiwania względem zachowania dolara kanadyjskiego w przeciągu tygodnia mogą być obarczone największym błędem.

Najmniej zmiennymi parami biorąc pod uwagę wszystkie parametry okazały się dolar australijski i dolar nowozelandzki, których tygodniowe notowania cechuje zarówno niska średnia i mediana, jak również odchylenie standardowe (najniższe w całym zestawieniu) oraz współczynnik zmienności.

Nieco ciekawsze informacje daje nam za do analiza rozkładu częstości, gdyż zapewnia nieco większy pogląd na to, jakich ruchów z jakim prawdopodobieństwem możemy oczekiwać w przypadku poszczególnych walut. Ważne założenie: zmiana dotyczy różnicy między tygodniowym High i Low, a więc nie uwzględnia kursów otwarcia i zamknięcia ani ich pozycji względem siebie.

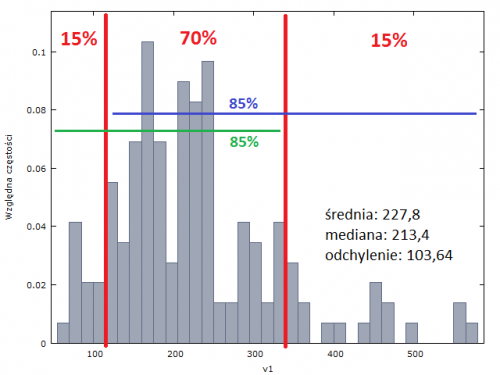
Wyliczone zmiany tygodniowe uszeregowane zostały w kolejności rosnącej, a następnie pogrupowane w przedziałach o szerokości 15 pipsów. Następnie rozkład podzielony w ten sposób, że odcięte zostały początkowe przedziały grupujące 15% najniższych wyników oraz końcowe przedziały o tej samej ilości najwyższych wyników. Celem takiej reorganizacji wyników jest zawężenie możliwych ruchów kosztem nieznacznej utraty pewności co do wystąpienia tych ruchów.

Daje nam to trzy informacje:

• około 70% wyników znajduje się pomiędzy wartością otwierającą pierwszy przedział, a wartością zamykającą ostatni przedział po odcięciu 15% skrajnych wyników,

• z 85-procentowym prawdopodobieństwem możemy liczyć na ruch o wielkości co najmniej wartości otwierający pierwszy przedział po odcięciu 15% najniższych wyników,

• z 85-procentowym prawdopodobieństwem możemy liczyć na ruch o wielkości nie przekraczającej wartości zamykającej ostatni przedział po odcięciu 15% najwyższych wyników.

Poglądowy wykres dla EURUSD:

W prostych słowach, wiemy (z 85-procentową pewnością) o ile co najmniej zmieni się kurs danej waluty, z tą samą pewnością wiemy jakiej wartości tygodniowy ruch nie przekroczy, oraz że w 70% przypadków tygodniowa zmiana znajdzie się pomiędzy tymi wartościami.

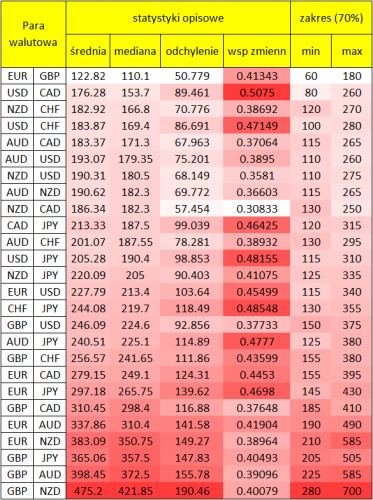
Z powyższej, lewej tabeli wynika, że w przypadku na przykład funta brytyjskiego, tygodniowy ruch w 85% przypadków przekroczył 150 pipsów, a więc na tyle co najmniej powinniśmy liczyć. Najmniejszej zmiany możemy oczekiwać zaś w przypadku CAD’a, dla którego tą granicą jest 80 pipsów. Kolejność w przypadku powyższej tabeli jest niemal taka sama jak w przypadku tabeli z medianą, co jest całkowicie normalne.

Gdy zaś zastanawiamy się, na jaki maksymalny, prawdopodobny ruch liczymy, wystarczy zajrzeć do prawej tabeli. Sugeruje ona, że w 85% przypadków ruch na funcie nie przekroczy 375 pipsów, czy 260 na dolarze kanadyjskim.

Co powyższe dane oznaczają w praktyce? Po pierwsze to, że jeżeli otwieramy pozycję na początku tygodnia i wiemy, że nie przetrzymamy jej przez weekend, możemy liczyć na ruch co najmniej około 115 pipsów (w zależności od konkretnej waluty) i co najwyżej około 300. Po drugie wiemy również, że po wykonaniu ruchu o wielkości około 350 pipsów dana para przekroczyła swój typowy zakres a potencjał do jego dalszej kontynuacji jest znacznie mniejszy.

Pomaga to zarówno określić potencjalną stratę, jak i zysk, na jaki możemy liczyć. Oczywiście otwierając pozycję na podstawie analizy technicznej odpowiednio redukujemy prawdopodobieństwo zrealizowania czarnego scenariusza. To jest naturalnie najważniejszy element strategii i z tego też powodu, warto zajrzeć do naszej Akademii i tam szlifować warsztat tradingowy.

Poniżej szczegółowa tabela dla 26 najpopularniejszych par walutowych, uszeregowana według wartości mediany:

Analiza statystyczna, obok analizy makro, jest drugim ważnym elementem tradingu, o którym analitycy techniczni chętnie zapominają. Zarówno znajomość fundamentów stojących za trendami, jak statystyczna specyfika notowań są niezbędne w doskonaleniu swojego warsztatu tradingowego. Stąd też, dogłębna analiza powyższych obliczeń i wniosków, jak i samodzielne badanie interesujących nas kwestii znacząco zwiększa poziom naszej handlowej świadomości i pozwala usprawnić, a także sprofesjonalizować trading.

Treści przedstawione w niniejszym serwisie zostały przygotowane z należytą starannością i w oparciu o najlepszą wiedzę ich autorów. Mają one charakter informacyjny i nie stanowią rekomendacji ani porady inwestycyjnej w rozumieniu Rozporządzenia Ministra Finansów z dnia 19 października 2005 r. (Dz. U. z 2005 r. Nr 206, poz. 1715) w sprawie informacji stanowiących rekomendacje dotyczące instrumentów finansowych, ich emitentów lub wystawców. Ich autorzy i serwis Investio.pl nie ponoszą odpowiedzialności za decyzje inwestycyjne podjęte na podstawie wyżej wymienionych treści, a w szczególności za straty z nich wynikłe.