Teoria Chaosu w analizie rynków finansowych

Powszechnie obowiązujący paradygmat finansowy opiera się na wielu założeniach oraz postulatach na których skonstruowano liczne modele ekonomiczne umożliwiające analizę ilościową rynku kapitałowego. Chcielibyśmy w tym miejscu omówić kilka podstawowych założeń na bazie których skonstruowano modele wyceny powszechnie używane przez wszystkich uczestników rynków finansowych, począwszy od inwestorów indywidualnych, a skończywszy na zarządzających aktywami funduszy inwestycyjnych. Analiza poszczególnych założeń ma na celu pokazanie zawodności i chwiejności teorii opartych na obecnym paradygmacie oraz wskazanie potrzeby poszukiwania alternatywnych metod analizy rynków finansowych.

Hipoteza efektywności rynku.

Jednym z podstawowych i najważniejszych, a jednocześnie najbardziej kontrowersyjnych założeń jest tak zwana hipoteza efektywności rynku, zakładająca rzetelną wycenę aktywów poprzez mechanizm rynkowy. Hipoteza ta, w skrócie, mówi o tym, iż każda nowa informacja pojawiająca się na rynku jest natychmiast inkorporowana, uwzględniona w cenie aktywów, dzięki czemu są one rzetelnie wycenione. Współczesne badania nad naturą rynków kapitałowych wskazują na nieliniowy charakter systemu gospodarczego (w systemach liniowych siła reakcji na dany bodziec jest wprost proporcjonalna do siły bodźca), oznacza to, że kolejne informacje napływające na rynek mogą być z początku ignorowane, by dopiero w pewnym punkcie kulminacyjnym ujawnić swój wpływ. Z nieliniowym charakterem systemu gospodarczego wiążą się takie własności jak efekt długotrwałej pamięci (dany proces przechowuje „pamięć” o informacjach przeszłych), czy też efekt sprzężenia zwrotnego (informacje przeszłe wpływają na przyszłość, natomiast nowe informacje wpływają na percepcję przeszłych obserwacji oraz oczekiwań co do przyszłości).

Powyższe cechy procesów gospodarczych przeczą tezie mówiącej o występowaniu zjawiska błądzenia przypadkowego na rynkach finansowych, w rzeczywistości ceny ulegają trendom, zachowują pamięć o przeszłych obserwacjach, są autoskorelowane i nie mają charakteru niezależnych zmiennych losowych.

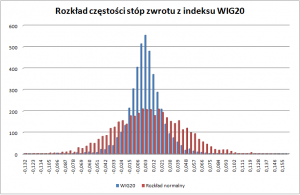
Zgodnie z obecną teorią ekonomii procesy stochastyczne opisujące kształtowanie się cen aktywów na rynkach finansowych cechują się gaussowskim rozkładem normalnym. Porównanie rozkładu stóp zwrotu różnych aktywów z rozkładem normalnym pokazuje iż w rzeczywistości rozkłady stóp zwrotu cechują się tzw. leptokurtycznością tzn. obserwacje bliskie średniej występują częściej niż w rozkładzie normalnym, oraz występuje zjawisko tzw. grubych ogonów, przy czym ogon lewy (ujemne stopy zwrotu) jest szerszy niż prawy. Naukowcy określają rozkłady tego typu jako stabilne rozkłady Pareto-Levy-ego, w takich przypadkach miary takie jak wartość oczekiwana oraz wariancja w sensie gaussowskim nie mają żadnej użyteczności.

Teoria racjonalnego inwestowania.

Kolejnym bardzo istotnym założeniem występującym w obecnym paradygmacie finansowym jest tzw. teoria racjonalnego inwestowania zgodnie z którą inwestorzy dokonują racjonalnych wyborów poprzez analizę danych historycznych. Psychologowie behawioralni Daniel Kahneman oraz Amos Tversky w swoich licznych pracach udowodnili, iż ludzie nie postępują racjonalnie, w ich decyzjach można spotkać wiele sprzeczności, wystarczy odwołać się do przykładu gdzie w zależności od kolejności zadawanych pytań ankietowani potrafili stwierdzić, że wolą jabłka od pomarańczy, pomarańcze od gruszek oraz preferują gruszki nad jabłka (sic!).

Analiza uproszczeń występujących w obecnym paradygmacie oraz uwypuklanie wad powszechnie obowiązującego paradygmatu finansowego nie jest celem tego serwisu, powyższe przykłady zostały podane, aby uświadomić użytkownikom chwiejność podstaw powszechnie nauczanej teorii ekonomii oraz finansów.

Wymienione powyżej założenia obecne we współczesnym paradygmacie finansowym umożliwiają analizę ilościową rynków kapitałowych, w szczególności stosowanie rozkładu prawdopodobieństwa (typu gaussowskiego). Powyższe przykłady świadczące o nieprawdziwości tych założeń świadczą o niskiej wartości użytkowej modeli zbudowanych w oparciu o obecny paradygmat, mowa tu o modelach powszechnie używanych przez uczestników rynków finansowych, modele te to np. model wyceny opcji Blacka-Scholesa, modele wyceny aktywów CAPM i APT, teoria portfelowa Markowitza i inne. Na wykresie przedstawiono rozkład częstości stóp zwrotu z indeksu WIG20 porównany z rozkładem wygenerowanym losowo.

Rys. 1, Porównanie rozkładu częstości stóp zwrotu indeksu WIG20 z rozkładem wygenerowanym losowo

Gdy uświadomimy sobie iż zjawiska występujące na rynkach finansowych nie podlegają rygorom szerzonym przez współczesny paradygmat, należy odwołać się do alternatywnych metod analizy systemów gospodarczych jakim niewątpliwie jest Teoria Chaosu.

Teoria Chaosu to bardzo młody dział nauki, powstały w XX wieku, jest to temat bardzo szeroki, celem tego serwisu nie jest przybliżanie użytkownikom idei tej nauki w sposób szczegółowy, gdyż jest to po prostu zbyt obszerny oraz skomplikowany dział wiedzy. Poniżej chcieliśmy przedstawić jedno z narzędzi analizy rynków kapitałowych wykorzystujące ideę Teorii Chaosu, tzw. analizę R/S. Z drugiej strony zachęcamy użytkowników do zaznajomienia się z literaturą tego tematu, gdyż okazuje się, iż teoria chaosu w sposób dość dokładny opisuje zjawiska występujące na rynkach finansowych, jak również zjawiska naturalne występujące w przyrodzie.

Więcej na temat analizy finansowej spółek giełdowych dowiesz się dzięki naszej dedykowanej aplikacji squaber.com oraz podczas jednego z organizowanych przez nas darmowych szkoleń online. Zapisy pod tym linkiem.