Model Blacka-Scholesa – założenia i definicja problemu
Najpopularniejszym modelem służącym do wyceny opcji jest model Blacka-Scholesa z 1973 roku opracowany przez Fischera Blacka oraz Myrona Scholesa. Uznano go za przełomowe podejście do określenia wartości tej klasy instrumentów finansowych, co doprowadziło ostatecznie do przyznania w 1997 roku Nagrody Banku Szwecji im. Alfreda Nobla w dziedzinie nauk ekonomicznych jego twórcom Robertowi Mertonowi oraz Myronowi Scholesowi. Fischer Black niestety nie dożył tej chwili.
W swojej pracy „Pricing of Options and Corporate Liabilities” Black i Scholes przedstawiają podejście do wyceny kontraktu opcyjnego, które bynajmniej nie jest pionierskie (o związanych z tym kontrowersjach pisałem już wcześniej w artykule „Niesłuszna nagroda nobla?„). Bardzo podobne koncepcje wyceny zostały przedstawione dużo wcześniej np. przez:
- Louisa Bacheliera[1] w 1900 roku,
- Casea Sprankla [2] w 1961 roku,
- Paula Samulesona [3] w 1965 roku,
- Andrew Chena [4] w 1970 roku.
Różnica polega na zastosowaniu innych założeń, które sprawiły, że aktualnie najbardziej rozpoznawalny model wyceny opcji jest modelem wygodnym i możliwym do zastosowania przez każdego. W modelu wyceny opcji na akcje nie przynoszące dochodu założenia te to[5]:
- Krótkoterminowa stopa procentowa jest znana i stała w czasie.
- Cena akcji jest odzwierciedlona przez proces błądzenia losowego w czasie ciągłym z wariancją proporcjonalną do kwadratu ceny. Implikuje to, że na końcu skończonego przedziału czasu możliwe ceny akcji mają rozkład logarytmiczno-normlany.
- Akcje nie przynoszą żadnego dodatkowego dochodu.
- Opcja jest typu europejskiego.
- Na rynku nie ma prowizji ani jakichkolwiek innych kosztów transakcyjnych.
- Walory są doskonale podzielne.
- Pożyczki są oprocentowane według krótkoterminowej stopy procentowej.
- Dozwolona jest krótka sprzedaż.
Przy takich założeniach cena opcji zależy od dwóch zmiennych – ceny akcji oraz czasu pozostałego do wygaśnięcia opcji. Pozostałe parametry są przyjmowane jako stałe.
Podsumowując, aby wyznaczyć teoretyczną wartości opcji na akcję należy określić zmienne oraz parametry, które mają na nią wpływ. W tym przypadku będą to:
- Cena spot instrumentu bazowego – X.
- Cena wykonania opcji – C.
- Termin wykonania opcji T, określony w jednostce czasu.
- Zmienność ceny spot instrumentu bazowego – σ.
- Wolna od ryzyka ciągła stopa procentowa – r.
W tak przyjętej konwencji należy w odpowiedni sposób ująć czas t pozostający do wygaśnięcia opcji, który w tym modelu jest zmienną niezależną. Będzie się on zmieniał w następującym przedziale [0, T].
Zgodnie z założeniem 2. cena akcji jest odzwierciedlona przez proces stochastyczny w czasie ciągłym (tj. dla Δt→0 ) zwanym geometrycznym ruchem Browna, danym w postaci następującego równania różniczkowego:
gdzie:
Załóżmy następnie, że budujemy portfel składający się z pozycji długiej w jednej akcji oraz pozycji krótkiej w 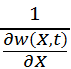 opcjach. Wartość kapitału E w takiej pozycji można zatem zapisać jako różnicę
opcjach. Wartość kapitału E w takiej pozycji można zatem zapisać jako różnicę 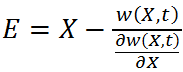 . Zakłada się również, że tak opisany portfel jest dostosowywany w czasie ciągłym do zmiany wielkości t i X. Przy tym założeniu stopa zwrotu z takiego portfela jest „pewna” i musi wynikać ze zmiany wartości pieniądza w czasie. W przeciwnym wypadku możliwy byłby arbitraż.
. Zakłada się również, że tak opisany portfel jest dostosowywany w czasie ciągłym do zmiany wielkości t i X. Przy tym założeniu stopa zwrotu z takiego portfela jest „pewna” i musi wynikać ze zmiany wartości pieniądza w czasie. W przeciwnym wypadku możliwy byłby arbitraż.
Jasnym jest, że w takim wypadku zmiana wartości opcji wynosi:
Równanie 2 spełnia założenia równania Ito[6], można je zatem zapisać w sposób następujący:
Zapisując zmianę kapitału jako 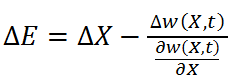 oraz podstawiając Równanie 3 otrzymuje się:
oraz podstawiając Równanie 3 otrzymuje się:
Z drugiej strony, jak wspomniano wyżej, zmianę wartości kapitału możemy ująć z punktu widzenia zmiany wartości pieniądza w czasie, wtedy:
Porównując stronami równania 4 oraz 5 dochodzi się do ostatecznej formy problemu, polegającego na wyznaczeniu formuły określającej teoretyczną wartość opcji na akcje:
Rozwiązanie tego problemu zostanie przedstawione w następnej kolejności.
[1] Bachelier, L., „Théorie de la spéculation”, Annales scientifiques de l’É.N.S. 3e série, tome 17, 1900, s. 21 – 86.
[2] Sprankle, C., „Warrant proces as indication sod expectations”, Yale Econ. Essays 1, 1961, s. 179 – 232.
[3] Samuelson, P., „Rational theory of warrant pricing”, Indus. Management Rev. 6, 1965, s. 13-31.
[4]Chen, A., „A model of warrant pricing in a dynamic market”, J. Finance 25, 1970.
[5] Black F., Scholes M., „The Pricing of Options and Corporate Liabilities”, Journal of Political Economy, Vol. 81, No. 3, (May/June 1973), s. 641.
[6] Więcej na ten temat w Weron, A., Weron, R., ”Inżynieria finansowa. Wycena instrumentów pochodnych. Symulacje komputerowe. Statystyka rynku”, Wydawnictwo Naukowo-techniczne, Warszawa 2005, s. 168 – 170 oraz http://en.wikipedia.org/wiki/It%C5%8D’s_lemma.
Tags: wycena opcji





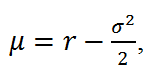
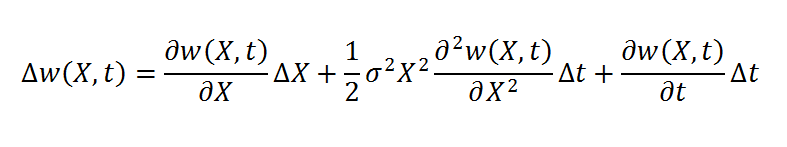
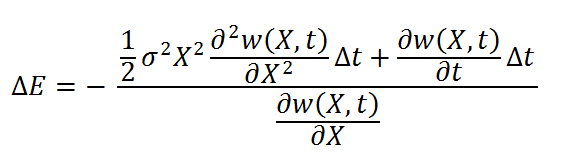
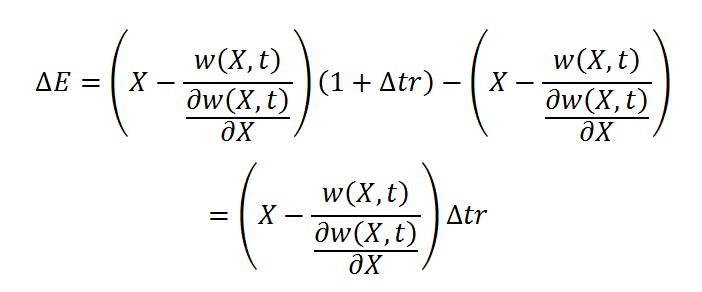
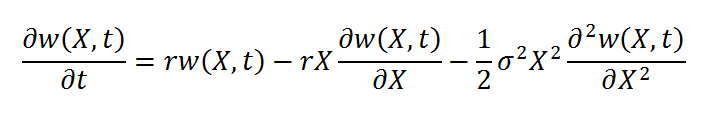



Komentarze 2
Model Blacka-Scholesa – wycena akcji nieprzynoszących dywidendy – Investio.pl
[…] założeniach omówionych w artykule “Model Blacka-Scholesa – założenia i definicja problemu“, wartość opcji kupna akcji niewypłacającej dywidendy jest zadana w pełni […]
Wycena opcji walutowych – wzór Garmana-Kohlhagena – Investio.pl
[…] modelu Blacka-Scholesa, którego wyprowadzenie zostało przedstawione w artykułach “Model Blacka-Scholesa – założenia i definicja problemu” oraz “Model Blacka-Scholesa – wycena akcji nieprzynoszących dywidendy“. […]