Metoda Monte Carlo

Metoda Monte Carlo służy do modelowania procesów złożonych, których rozwiązanie w sposób analityczny jest niemożliwy, lub zbyt czasochłonny. Metoda została opracowana przez zespół znanego matematyka Johna von Neumanna podczas II wojny światowej. Jej pierwszym zastosowaniem było modelowanie procesów dyfuzji neutronów (źródło).

Symulacje Monte Carlo stanowią jedno z narzędzi matematyki numerycznej, kluczowym zagadnieniem związanym z tą metodą jest losowość wielkości charakteryzujących dane zjawisko. Podstawowym założeniem związanym z wykorzystaniem tej metody jest znajomość rozkładu danej zmiennej opisującej proces stochastyczny – w przypadku próby zastosowania metody Monte Carlo na rynkach finansowych musimy zdać sobie sprawę z jak problematycznym zagadnieniem mamy do czynienia, więcej o tym tutaj.

Wpis nie ma charakteru naukowego i nie opisuje w sposób szczegółowy metody symulacyjnej Monte Carlo, w przypadku poszukiwania podstawowych informacji zachęcam do skorzystania z odpowiedniej literatury. W tym miejscu chciałbym jedynie pokazać na przykładzie  sposób wykorzystania metody Monte Carlo oraz zasygnalizować gdzie ta metoda jest wykorzystywana na rynkach finansowych.

Jednym z zastosowań powyższej metody symulacyjnej jest obliczanie całek oznaczonych dla poszczególnych funkcji.  Jak to zrobić? Poniżej, na przykładzie chciałbym przedstawić symulację takich obliczeń dla całki oznaczonej o granicach 0 do 1 funkcji potęgowej f(x) = x^4. Generalnie obliczenie całki z tego typu funkcji zajmuje kilka sekund (=0,2), jednak na takim przypadku chciałbym zademonstrować sposób działania metody Monte Carlo, któryą każdy z Was może wykorzystać w bardzo prosty sposób posiadając jedynie dostęp do Excela. Wystarczy odrobina znajomości języka Visual Basic, poniżej wklejam fragment kodu i wygląd arkusza.

Rysunek 1. Wygląd arkusza – liczenie całki oznaczonej (0,1) funkcji potęgowej y=x^4 (źródło: opracowanie własne)

Poniżej fragment kodu, potrzebny do wygenerowania całki oznaczonej opisywanej powyżej:

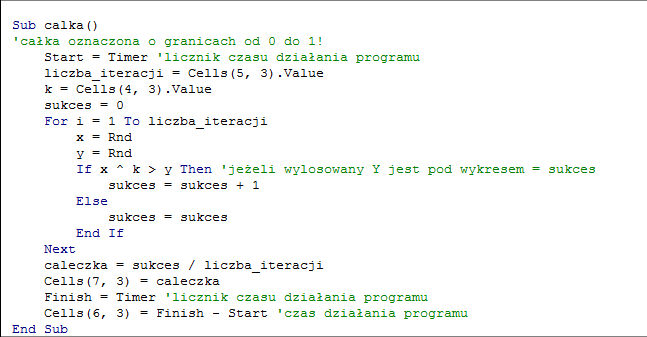
Rysunek 2. Kod Visual Basic potrzebny do wygenerowania całki oznaczonej (0,1) funkcji potęgowej y=x^4 (źródło: opracowanie własne)

Jak działa nasz algorytm? Całka oznaczona jest pojęciem tożsamym z polem pod wykresem funkcji. Nasz algorytm losuje 10 000 000 punktów x,y z iloczynu kartezjańskiego (0,1) x (0,1), a następnie sprawdza ile wylosowanych w ten sposób punktów znajduje się pod wykresem funkcji f(x) = x^4. Iloraz liczby punktów spełniających te warunki przez liczbę iteracji ogółem jest symulacją Monte Carlo pola pod wykresem tej funkcji oraz jednocześnie symulacją jej całki oznaczonej od 0 do 1. Jak widać kod potrzebny do symulowania całek jest bardzo krótki, a czas pracy algorytmu wyniósł niewiele ponad 4 sekundy, błąd przy 10 milionach iteracji znajduje się dopiero na piątym miejscu po przecinku, jeżeli kogoś interesują bardziej dokładne pomiary wystarczy jedynie zwiększyć liczbę iteracji.

Opisywany powyżej przypadek jest oczywiście bardzo prostym przykładem, omawianą całkę można obliczyć w pamięci w kilka sekund, jednak idea symulacji Monte Carlo dla bardziej skomplikowanych całek jest taka sama, wystarczy dokonać jedynie drobnych zmian w kodzie, a w bardzo prosty i szybki sposób znajdziemy rozwiązanie problemów, z którymi nie bylibyśmy w stanie sobie poradzić stosując rozwiązania analityczne.

Symulacje Monte Carlo, w dobie rosnącej mocy obliczeniowej komputerów są świetną (i bardzo prostą) alternatywą dla skomplikowanych metod analitycznych w przypadku rozwiązań bardzo skomplikowanych problemów. Potencjalnymi wadami tej metody jest   np. niska jakość generatora liczb pseudolosowych. Symulacje Monte Carlo dają jedynie przybliżone wyniki, nie mogą być stosowane do problemów wymagających dokładnych, „idealnych” odpowiedzi.

Opisywana przeze mnie metoda jest dość powszechnie wykorzystywana na rynkach finansowych, bardzo często stosuje się ją w przypadku wycen opcji.