Model Blacka-Scholesa – wycena akcji nieprzynoszących dywidendy
Przy założeniach omówionych w artykule „Model Blacka-Scholesa – założenia i definicja problemu„, wartość opcji kupna akcji niewypłacającej dywidendy jest zadana w pełni parabolicznym, cząstkowym równaniem różniczkowym w postaci:
z warunkiem początkowym, będącym funkcją wypłaty z opcji w terminie jej wygaśnięcia
Istnieje taka zamiana zmiennych X i t na odpowiednio u i τ:
oraz takie podstawienie za funkcję W(X,t) funkcji y(υ, τ) w postaci:
które sprowadza problem wyjściowy do postaci szczególnego, parabolicznego równania różniczkowego zwanego równaniem przewodnictwa cieplnego[1].
Taka zdefiniowany problem implikuje rozwiązanie w charakterystycznej, wygodnej i znanej postaci wzoru Blacka-Scholesa dla opcji kupna
gdzie:
Natomiast dla opcji sprzedaży
Proces przekształcenia Równania 1 w Równanie 7 został w pełni przedstawiony w pliku „Model Blacka-Scholesa – wyprowadzenie„.
Taka postać równań na wartość opcji kupna i sprzedaży akcji nieprzynoszących dochodów niesie za sobą kilka konsekwencji, które sprawiły, że jest on tak rozpoznawalny i wszedł do kanonu ekonomii. Co więcej, wzory te sprawiły, że wcześniej wspominane formuły wyceny opcji przeszły do historii. Stało się tak między innymi dlatego, że Black i Scholes wprowadzili dodatkowe założenia, które uczyniły ich model jeszcze bardziej specyficznym, ale jednocześnie wygodniejszym. Dla przykładu formuła przedstawiona przez Sprankle’a w 1961 dla opcji kupna na akcje wyglądała w sposób następujący[2]:
Równanie 9 różni się od równania 7 występowaniem parametrów k oraz k*. Pierwszy z nich, według Spranklea, jest ilorazem oczekiwanej wartości akcji w dniu wygaśnięcia opcji i aktualnej ceny akcji. Drugi natomiast jest czynnikiem dyskontującym odzwierciedlającym ryzyko danego waloru. Sprankle próbował wyznaczać wartości k oraz k* empirycznie, ale okazało się to niemożliwe. Kolejne próby przedstawiania poprawnego wzoru na wycenę opcji były rzecz jasna rozwinięciem tej koncepcji[3].
Wartym podkreślenia jest tu wkład Sprankle’a w wycenę opcji w ogóle. Jako pierwszy zastosował on rozkład logarytmiczno-normalny jako lepiej opisujący zmiany cen akcji w ujęciu wartościowym.
Przełomowym stało się podejście Blacka i Scholesa, wynikające z tak zwanego dynamicznego delta – hedgingu przeprowadzanego w czasie ciągłym, o czym pisałem w artykule „Model Blacka-Scholesa – założenia i definicja problemu„. Pozwoliło to wyeliminować z równań parametry określające oczekiwaną stopę zwrotu z akcji, co doprowadziło formułę wyceny do de facto funkcji dwóch zmiennych – aktualnej ceny waloru X oraz czasu pozostającego do wygaśnięcia opcji t, tak jak przedstawiają to Równania 7 oraz 8. Innymi słowy jeżeli dynamiczny delta – hedging jest utrzymywany w czasie ciągłym oczekiwana stopa zwrotu z takiej pozycji musi być równa krótkoterminowej stopie procentowej r.
Założenie o dynamicznym delta-hedgingu w czasie ciągłym z jednej strony sprawia, że wzór Blacka-Scholesa jest bardzo elegancki, co jest jego niewątpliwą zaletą. Z drugiej strony sprawia ono, że model w pewnych warunkach rynkowych jest bardzo wrażliwy na zmiany parametrów, co zostanie omówione w kolejnych artykułach.
Więcej na temat analizy finansowej spółek giełdowych dowiesz się dzięki naszej dedykowanej aplikacji squaber.com oraz podczas jednego z organizowanych przez nas darmowych szkoleń online. Zapisy pod tym linkiem.
[1] Brown, J. W., Churchill R. V., “Fourier series and boundary value problems”, McGraw-Hill Inc. 1993, s. 137.
[2] Sprankle, C., „Warrant prices as indications of expectations”, Yale Econ. Essays 1, 1961, s. 179 – 232
[3] Ściślej rzecz ujmując koncepcji Bacheliera z tym, że przy założeniu rozkładu logarytmiczno-normalnego cen akcji.
Tags: wycena opcji









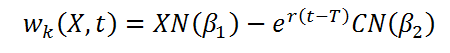

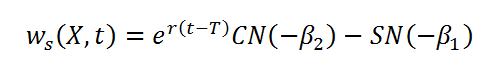




Komentarze 1
Wycena opcji walutowych – wzór Garmana-Kohlhagena – Investio.pl
[…] “Model Blacka-Scholesa – założenia i definicja problemu” oraz “Model Blacka-Scholesa – wycena akcji nieprzynoszących dywidendy“. Modyfikacją jest w tym wypadku wprowadzenie kolejnego parametru, jakim jest stopa wolna od […]