Wycena opcji walutowych – wzór Garmana-Kohlhagena
Model wyceny opcji walutowych jest analogiczny do „podstawowego” modelu Blacka-Scholesa, którego wyprowadzenie zostało przedstawione w artykułach „Model Blacka-Scholesa – założenia i definicja problemu” oraz „Model Blacka-Scholesa – wycena akcji nieprzynoszących dywidendy„. Modyfikacją jest w tym wypadku wprowadzenie kolejnego parametru, jakim jest stopa wolna od ryzyka w kraju waluty kwotowanej.
Zakładamy, że wycenie podlega opcja kupna #EURPLN. W związku z tym wprowadzone zostają nowe oznaczenia:
- rd – wolna od ryzyka stopa procentowa w kraju waluty kwotowanej[1],
- rf – wolna od ryzyka stopa procentowa w kraju waluty bazowej.
Pozostałe parametry są takie same jak w przypadku wyceny opcji na akcje.
Rozumowanie jakie przeprowadzili Mark Garman i Steven Kohlhagen w 1983 roku[2] zakłada, że stosunek premii za ryzyko do ryzyka mierzonego odchyleniem standardowym jest taki sam dla walut i opcji na waluty i wynosi λ. Zatem można zapisać, że:
oraz
gdzie
– μ – „dryf” kursu spot wymiany,
– α – oczekiwana stopa zwrotu z opcji,
– σα – odchylenie standardowe oczekiwanej stopy zwrotu z opcji.
Następnie przeprowadzając analogiczną procedurę tzw. ciągłego delta-hedgingu do tej opisanej równaniami od 1 do 3 w artykule „Model Blacka-Scholesa – założenia i definicja problemu„, przy ponownym zastosowaniu lematu Ito, otrzymuje się różniczkowe równanie cząstkowe w następującej postaci:
Równanie 3 jest równaniem podobnym do Równania 6 z artykułu „Model Blacka-Scholesa – założenia i definicja problemu” w związku z tym, że zastosowano w nim niemal identyczną logikę założeń. Jego rozwiązanie jest analogiczne do rozwiązania zaproponowanego przez Roberta Mertona[3] w jego modelu wyceny opcji na akcje wypłacające dywidendę w wielkości proporcjonalnej do ceny akcji. W wypadku opcji walutowych założenie o proporcjonalności oprocentowania posiadanej waluty obcej wydaje się być założeniem mniej abstrakcyjnym, niż proporcjonalność dywidendy w stosunku do ceny akcji.
Rozwiązaniem Równania 3 jest cena europejskiej opcji kupna wystawionej na określoną parę walutową. Dane jest ona następującym wzorem:
gdzie:
Dla opcji sprzedaży natomiast:
Równania 4 i 5 będą wykorzystywane w dalszych aktykułach do obliczenia teoretycznej wartości opcji kupna i sprzedaży wystawianych na różne pary walutowe jak również do badania wrażliwości takiej wyceny.
[1] Stopa rd zastępuje w modelu wyceny opcji walutowych stopę r w modelu wyceny opcji na akcje omawianego wcześniej.
[2] Garman, B. M., Kohlhagen S. W., ”Foregin currency options values”, Journal of International Money and Finance, 1983, s. 231 – 237.
[3] Merton, R., Samuelson, P., “A complete model of warrant pricing that maximizes utility”, Industrial Management Review, 1969.
Tags: wycena opcji






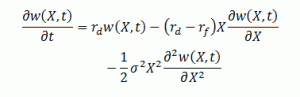




Komentarze 0